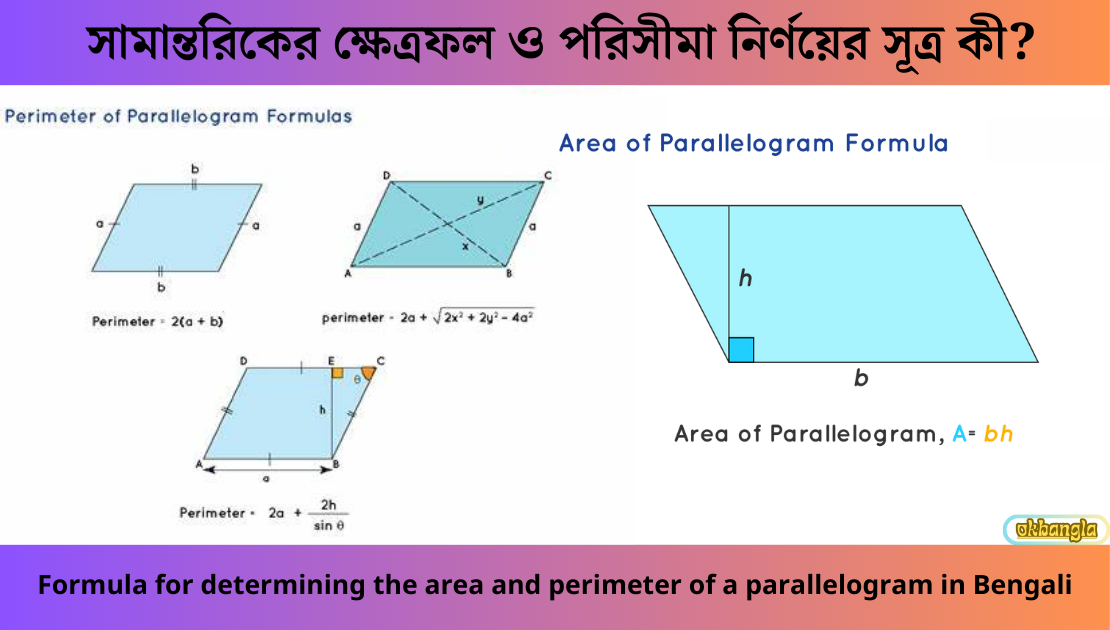
যে চতুর্ভূজের বিপরীত বাহুগুলো পরস্পর সমান্তরাল তাকে সামান্তরিক বলে। এই সামন্তরিকের বিভিন্ন বৈশিষ্ট রয়েছে, যেমন, সামান্তরিকের সন্নিহিত কোণ দুইটি পরস্পর সম্পূরক কোণ। এইসব বিষয়ে গণিতের ক্ষেত্রে অনেকেই হয়তো শিখে থাকবেন।
তবে একটা কথা সকলেই জানি যে, স্কুল জীবনের গণিত বইয়ে পরা সামান্তরিক এবং এর বিভিন্ন সূত্র প্রয়োগ শুধুমাত্র পরীক্ষার খাতায় লেখা সমাধানগুলোর মধ্যেই শেষ হয়ে যায় নি।
আমাদের বিভিন্ন সময় বেশ কিছু কাজে এই সূত্রগুলো ব্যবহার করতে হয়েছে। এমনকি কর্মজীবনের বিভিন্ন ক্ষেত্রেও এর ব্যবহার হয়।
তাই স্কুল শিক্ষার্থী থেকে শুরু করে বিভিন্ন ক্ষেত্রে কর্মরত ব্যক্তিদেরকেও সামান্তরিকের বিভিন্ন সূত্র জেনে রাখতে হবে। তাই আজকের এই প্রতিবেদনে আমরা সামান্তরিকের বিভিন্ন দিক নিয়ে আলোচনা করবো।
সামান্তরিক বলতে কি বুঝ? What do you mean by parallelogram?
সমতল জ্যামিতিতে সামন্তরিক হল এমন একটি চতুর্ভুজ যার বিপরীত বাহুদ্বয় পরস্পর সমান ও সমান্তরাল। তাই আয়তক্ষেত্র, বর্গ, রম্বস – প্রত্যেকে এক একটি সামন্তরিক, কেননা এদের প্রত্যেকটির নিজস্ব বিপরীত বাহুদ্বয় পরস্পর সমান ও সমান্তরাল হয়।
সামান্তরিকের কিছু বৈশিষ্ট্য, Some properties of parallelogram :
- সামান্তরিকের বিপরীত বাহুগুলি সমান এবং সমান্তরাল।
- সামান্তরিকের বিপরীত কোণগুলি সমান।
- সামান্তরিকের কর্ণগুলি পরস্পর সমান এবং পরস্পরকে সমদ্বিখণ্ডিত করে।
- সামান্তরিকের প্রতিটি কোণের পরিমাপ ১৮০°।
- সামান্তরিকের যে কোন কর্ণ সামান্তরিকটিকে দুইটি সর্বসম ত্রিভুজে বিভক্ত করে।
- সামান্তরিকের একটি কর্ণ এর অপর কর্ণ দ্বারা সমদ্বিখণ্ডিত হয়।
- সামান্তরিকের ক্ষুদ্রতর কর্ণ দ্বারা সামান্তরিকটি যে দুইটি ত্রিভুজে বিভক্ত হয় সেই ত্রিভুজ দুইটির উভয়ই সূক্ষ্মকোণী ত্রিভুজ।
- সামান্তরিকের চারটি কোণের সমষ্টি চার সমকোণ বা ৩৬০°।
- সামান্তরিকের কর্ণ হল সামান্তরিকটির দুইটি বিপরীত কৌণিক বিন্দুর দুরত্ব।
- সামান্তরিকের কর্ণদ্বয় সামান্তরিকটিকে চারটি সমান ক্ষেত্রফলবিশিষ্ট ত্রিভুজে বিভক্ত করে।
- সামান্তরিকের প্রত্যকটি কোণ সমকোণ হলে তখন এটি আয়তক্ষেত্র।
- সামান্তরিকের কোণগুলো সমকোণ হলে এবং বাহুগুলো পরস্পর সমান হলে তখন এটি বর্গক্ষেত্র।
একটি সমান্তরালগ্রামের প্রয়োজনীয়তা পূরণ করে এমন চারটি আকার হল বর্গক্ষেত্র, আয়তক্ষেত্র, রম্বস এবং রম্বস । একটি রম্বস দেখতে একটি তির্যক বর্গক্ষেত্রের মতো এবং একটি রম্বস দেখতে একটি তির্যক আয়তক্ষেত্রের মতো।
সামান্তরিকের ক্ষেত্রফল কত? What is the area of the parallelogram?
সামান্তরিকের ক্ষেত্রফল হল একটি সামান্তরিক চারটি বাহু দ্বারা কতটা জায়গা বা সমতল অংশ দখল করে আছে তার মান। সামান্তরিক ক্ষেত্রফল একাধিকভাবে নির্ণয় করা যায়।
সংক্ষেপে বলতে গেলে সামন্তরিকের ক্ষেত্রফল = ভুমি × উচ্চতা।
একটি সমান্তরালগ্রামের ক্ষেত্রফল বের করার সূত্র হল A = bh , যেখানে b হল ভিত্তি এবং h হল সমান্তরালগ্রামের উচ্চতা। একটি সমান্তরালগ্রাম একটি বর্গক্ষেত্র, একটি আয়তক্ষেত্র, একটি রম্বস, বা যে কোন আকৃতি হতে পারে যার বিপরীত বাহুগুলি সমান্তরাল।
কর্ণের সাহায্যে সামান্তরিকের ক্ষেত্রফল নির্ণয়? Find the area of the parallelogram with the help of hypotenuse?
একটি সমান্তরালগ্রামের ক্ষেত্রফল গণনা করা যেতে পারে যখন কর্ণ এবং তাদের ছেদকারী কোণ জানা যায়। সূত্রটি দেওয়া হয়েছে, ক্ষেত্রফল = ½ × d 1 × d 2 sin (x) , যেখানে ‘d1’ এবং ‘d2’ সমান্তরালগ্রামের কর্ণের দৈর্ঘ্য এবং ‘x’ হল তাদের মধ্যবর্তী কোণ।
সামান্তরিকের কর্ণদ্বয় কি সমান? Are the diagonals of a parallelogram equal?
সামান্তরিকের কর্ণদ্বয় পরস্পর সমান হলে কোণগুলো সমকোণ হয়। যে সামান্তরিকের একটি কোণ সমকোণ তা একটি আয়ত।
সামান্তরিকের বৃহত্তম কোণের মান কত? What is the value of the largest angle of the parallelogram?
একটি সামান্তরিকের বৃহত্তর কোণটি ক্ষুদ্রতর কোণের 3 গুণের থেকে 20 ∘ বেশি।
সামান্তরিকের পরিসীমা সূত্র, Formula for determining the range of parallelograms :
সামান্তরিকের প্রতিটি বাহুর সমষ্টিকে সামান্তরিকের পরিসীমা বলা হয়। একটি সামান্তরিকের সন্নিহিত যে কোন দুটি বাহুর মান জানা থাকলে সামান্তরিকের পরিসীমা সহজেই নির্ণয় করা যায়।
উদাহরণস্বরূপ, মনে করি যে একটি সামান্তরিকের সন্নিহিত বাহু দুইটি a এবং b। আমরা যেহেতু জানি, সামান্তরিকের বিপরীত বাহুগুলো পরস্পর সমান। তাই সামান্তরিকের পরিসীমা হবে-
P = (a+b+a+b) একক
বা, P = (২a+২b) একক
∴ P = ২(a+b) একক
সামান্তরিকের কর্ণের সূত্র, Formula for finding the hypotenuse of a parallelogram :
সামান্তরিকের কর্ণ হল যেকোনো সামান্তরিকের দুইটি বিপরীত কৌণিক বিন্দুর দুরত্ব। উক্ত দুরত্ব নির্ণয় করতে সামান্তরিকের কর্ণ নির্ণয়ের সূত্র জানতে হবে।
যদি মনে করা হয় যে, একটি সামান্তরিকের সন্নিহিত বাহু দুইটি a ও b এবং তাদের অন্তর্ভূক্ত কোণ θ; সেক্ষেত্রে সুতরাং, সামান্তরিকের কর্ণ d = √(a² + b²- 2ab cosθ)।
সামন্তরিক এবং আয়তক্ষেত্রের পরিসীমা নির্ণয়ের সূত্রে কি পার্থক্য আছে? What is the difference between the formula for determining the range of parallelogram and rectangle?
সামন্তরিক এবং আয়তক্ষেত্রের পরিসীমা নির্ণয়ে করার সূত্রে কোনো পার্থক্য নেই; উভয়ের ক্ষেত্রেই পরিসীমা নির্ণয়ের সূত্র হল: ২(দৈর্ঘ্য + প্রস্থ)।
পরিসীমা নির্ণয়ের সূত্র ছাড়াও সামন্তরিকের কোন বৈশিষ্ট্য জানলে এর পরিসীমা নির্ণয় করা যায়? What characteristics of the parallelogram can be used to determine its range?
সামন্তরিকের পরিসীমা নির্ণয় করতে সূত্র প্রয়োগ করার জন্য এর দৈর্ঘ্য এবং প্রস্থ জানা প্রয়োজন। তবে, যদি সামন্তরিকের একটি বাহুর দৈর্ঘ্য এবং কোনও কোণের মান জানা থাকে, সেক্ষেত্রেও ত্রিকোণমিতির সাহায্যে অন্য বাহুর দৈর্ঘ্য নির্ণয় করা যায়, এভাবে দৈর্ঘ্য জেনে পরিসীমা জানা সম্ভব হতে পারে। এটি করতে গেলে অবশ্যই গাণিতিক জ্ঞান এবং ত্রিকোণমিতির প্রয়োগ আবশ্যক।
শেষ কথা, Conclusion :
জ্যামিতি, পরিমিতি, ত্রিকোণমিতি ইত্যাদির বিভিন্ন সূত্র প্রয়োগ তথা সূত্রগুলো জেনে রাখা খুব জরুরি। বিভিন্ন সময়ে এই সূত্রগুলো আমাদের কাজে আসে। কিছু পরিমাপ করার ক্ষেত্রে হোক কিংবা পরীক্ষায় খাতায় সমান্তরাল সংক্রান্ত প্রশ সমাধানই হোক না কেনো, সমান্তরালে পরিসীমা ও ক্ষেত্রফল সূত্র জানা থাকা জরুরি।
আশা করি আজকের প্রতিবেদনের মাধ্যমে আপনারা সামান্তরিক কাকে বলে ? সামান্তরিকের ক্ষেত্রফল নির্ণয়ের সূত্র, সামান্তরিকের পরিসীমা নির্ণয়ের সূত্র, ইত্যাদি বিষয়ে বিস্তারিত জানতে পেরেছেন।
Frequently Asked Questions :
সামান্তরিকের ভূমিকে উচ্চতা দিয়ে গুণ করলে ক্ষেত্রফল পাওয়া যায়। সামান্তরিকের ক্ষেত্রফল এর যে কোন কর্ণদ্বারা গঠিত ত্রিভুজক্ষেত্রের ক্ষেত্রফলের দ্বিগুণের সমান।
সামন্তরিকের পরিসীমা নির্ণয়ের সূত্র হল: ২(দৈর্ঘ্য + প্রস্থ)। এখানে, দৈর্ঘ্য এবং প্রস্থ উভয়ই সামন্তরিকের দুই বিপরীত বাহুর দৈর্ঘ্য।
কোনো পার্থক্য নেই।