বিভিন্ন জ্যামিতিক আকৃতি গুলোর মধ্যে আয়তক্ষেত্র অন্যতম। আয়তক্ষেত্র সম্পর্কে জানাটা গুরুত্বপূর্ণ এই কারণে যে এটা বিভিন্ন সময়, নানা সমস্যার সমাধান এবং কিছু বিশেষ কাজে সাহায্য করবে। তাছাড়া বিদ্যালয়ের বিভিন্ন শ্রেনীর গণিত এর বইতে আয়তক্ষেত্রের পরিসীমা নির্ণয়ের সূত্র সংক্রান্ত প্রশ্নও রয়েছে। তবে সূত্র না জানলে সেগুলো সমাধান করা কঠিন, তাই আজকের এই প্রতিবেদনের মাধ্যমে আয়তক্ষেত্রের পরিসীমা নির্ণয় করা নিয়ে আলোচনা করবো।
আয়তক্ষেত্র কাকে বলে? What is a rectangle?
চতুর্ভুজের বিপরীত বাহুগুলো পরস্পর সমান ও সমান্তরাল এবং প্রত্যেকটি অন্তঃস্থ কোণ সমকোণ বা ৯০ ডিগ্রি হলে তাকে আয়ত বলে। আয়ত দ্বারা আবদ্ধ ক্ষেত্রকে আয়তক্ষেত্র বলে। আয়তক্ষেত্রের সরল সংজ্ঞা হিসেবে বলা যায়, যে চতুর্ভুজের বিপরীত বাহুগুলো পরস্পর সমান এবং প্রত্যেকটি কোণ সমকোণ তাকে আয়তক্ষেত্র বলে।
আয়তক্ষেত্রের বৈশিষ্ট্য, Properties of rectangles :
আয়তক্ষেত্রের ছোট দিকটিকে এর প্রস্থ (প্রস্থ) এবং দীর্ঘ দিকটিকে দৈর্ঘ্য বলা হয়। আয়তক্ষেত্রের সমস্ত কোণ সমকোণ। এটির চারটি বাহু এবং চারটি শীর্ষবিন্দু রয়েছে । প্রতিটি শীর্ষে 90 ডিগ্রির সমান কোণ রয়েছে। বিপরীত দিকগুলি সমান এবং সমান্তরাল। তির্যক একে অপরকে দ্বিখণ্ডিত করে। পরিধি এর দৈর্ঘ্য ও প্রস্থের যোগফলের দ্বিগুণের সমান।
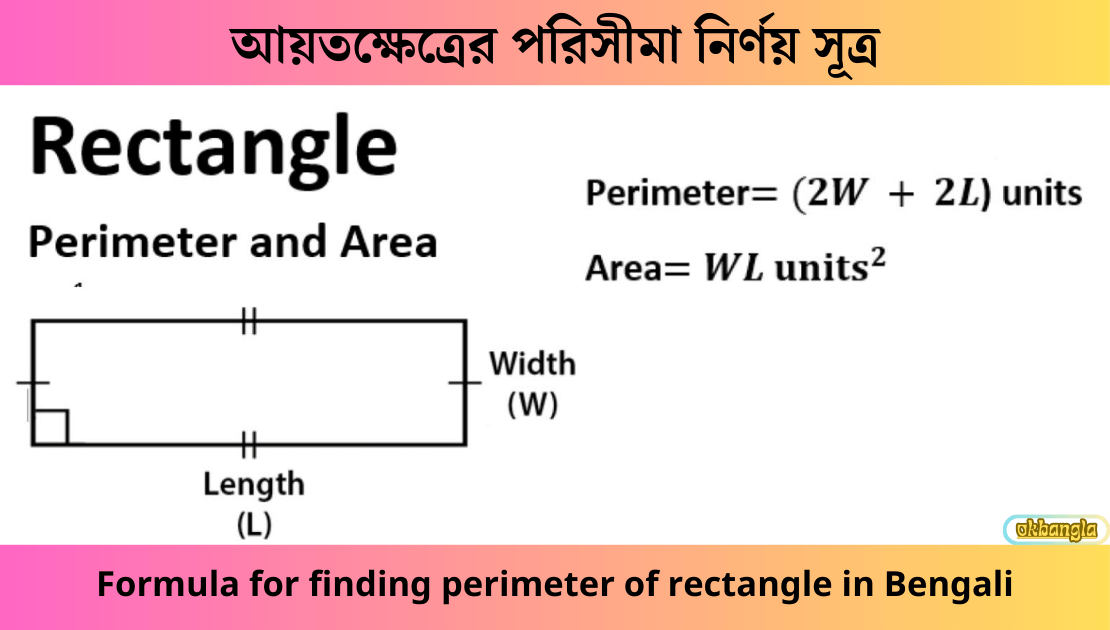
আয়তক্ষেত্রের পরিসীমা নির্ণয়ের সূত্র কি? What is the formula for determining the perimeter of a rectangle?
আয়তক্ষেত্রের পরিসীমা বলতে বুঝায় এর চারদিকের সীমানার দৈর্ঘ্য। যেহেতু আয়তক্ষেত্রের বিপরীত বাহুগুলো পরস্পর সমান, তাই এর একজোড়া সন্নিহিত বাহুর দৈর্ঘ্যের সমষ্টিকে দ্বিগুণ করলে পরিসীমা পাওয়া যায়।
এর থেকে বোঝা যায় যে, একটি আয়তক্ষেত্রের পরিসীমা মূলত আয়তক্ষেত্রের চারটি বাহুর যোগফল। একটি আয়তক্ষেত্র যে চারটি বাহু নিয়ে গঠিত হয় সেই চারটি বাহুর যোগফলই হবে ওই আয়তক্ষেত্রের পরিসীমা।
পরিসীমা মানে হল দুই মাত্রা বা পরিসরের একটি আকৃতির চারপাশের পথের মোট দৈর্ঘ্য। বৃত্তের ক্ষেত্রে এই পরিসীমাকে পরিধি বলা হয়।
আয়তক্ষেত্রের দৈর্ঘ্য = x সেমি এবং প্রস্থ = y সেমি। অতএব, পরিসীমা = 2(x + y) সেমি। আবার, ক্ষেত্রফল = xy বর্গ সেমি. আয়তক্ষেত্রের দৈর্ঘ্য = x সেমি এবং প্রস্থ = y সেমি।
অর্থাৎ আয়তক্ষেত্রের পরিসীমা হচ্ছে ওই আয়তক্ষেত্রের দৈর্ঘ্য এবং প্রস্থ এর যোগফলের দ্বিগুণ।
আয়তক্ষেত্রের ক্ষেত্রফল নির্ণয়ের সূত্র কি ? What is the formula for determining area of rectangle?
আয়তক্ষেত্রের ক্ষেত্রফল বলতে বুঝায় এর মাঝে কতটুকু অংশ আছে, অর্থাৎ সরল কথায় বলতে গেলে আয়তক্ষেত্রটি সমতলের কতটুকু স্থান দখল করে আছে।
কোনো একটি আয়তক্ষেত্রের দৈর্ঘ্যকে প্রস্থ দ্বারা গুণ করলে আয়তক্ষেত্রের ক্ষেত্রফল পাওয়া যাবে। যেহেতু ক্ষেত্রফল দ্বিমাত্রিক জ্যামিতির অন্তর্গত, সেক্ষেত্রে মনে রাখা উচিত ক্ষেত্রফলের সাথে উচ্চতার কোন সম্পর্ক নেই।
একটি আয়তক্ষেত্রের দৈর্ঘ্য এবং প্রস্থের গুণফলই হল সেই আয়তক্ষেত্রের ক্ষেত্রফল। আয়তক্ষেত্রের ক্ষেত্রফল = (দৈর্ঘ্য × প্রস্থ) বর্গ একক।
উদাহরণ স্বরূপ বলা যায়, যদি একটি আয়তক্ষেত্রের দৈর্ঘ্য 3 মিটার হয় ও এর প্রস্থ 2 মিটার হয়; সেক্ষেত্রে ওই আয়তক্ষেত্রের ক্ষেত্রফল হবে (3 × 2) বর্গ মিটার অর্থাৎ ৬ বর্গমিটার।
আয়তক্ষেত্রের কর্ণের দৈর্ঘ্য নির্ণয়ের সূত্র কি? What is the formula for determining the length of a rectangle’s diagonal?
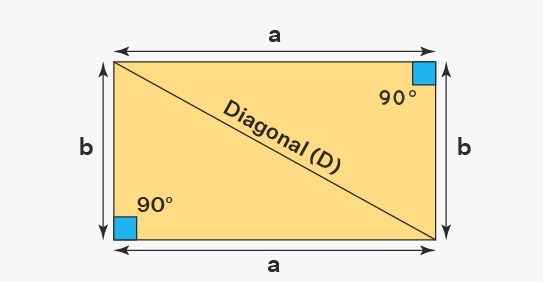
কোনো একটি আয়তক্ষেত্রের যে কোন দুইটি বিপরীত শীর্ষের সংযোজক রেখাংশটিকে আয়তক্ষেত্রের কর্ণ বলে। আয়তক্ষেত্রের বিপরীত শীর্ষগুলোকে যোগ করলে দুইটি রেখাংশ পাওয়া যায়। তাই একটি আয়তক্ষেত্রের দুইটি কর্ণ থাকে।
বলাই বাহুল্য যে, আয়তক্ষেত্রের কর্ণ দ্বারা আয়তক্ষেত্রটি দুইটি সর্বসম ত্রিভুজে বিভক্ত হয়। অন্যদিকে উৎপন্ন ত্রিভুজ দ্বয় সমকোণী ত্রিভুজ হয় এবং প্রত্যেকটি ত্রিভুজের ক্ষেত্রফল আয়তক্ষেত্রের ক্ষেত্রফলের অর্ধেক হয়।
জেনে রাখা ভালো যে, আয়তক্ষেত্রের কর্ণদ্বয়ের দৈর্ঘ্য পরস্পর সমান। পাশাপাশি, আয়তক্ষেত্রের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে।
কোনো আয়তক্ষেত্রের কর্ণের দৈর্ঘ্য নির্ণয় করার জন্য ব্যবহৃত সূত্রটি হল √{(দৈর্ঘ্য)² + (প্রস্থ)²}; এর থেকে আপনারা হয়তো বুঝতেই পারছেন যে দৈর্ঘ্য এবং প্রস্থ উভয়ের বর্গের যোগফল এর বর্গমূল হল একটি আয়তক্ষেত্রের কর্ণের দৈর্ঘ্য। এভাবেই আয়তক্ষেত্রের কর্ণের দৈর্ঘ্য বের করা যায়।
উদাহরণ হিসেবে বলা যায়, একটি আয়তক্ষেত্রের দৈর্ঘ্য যদি 3 মিটার হয়, আর প্রস্থ 2 মিটার হলে, সেক্ষেত্রে ওই আয়তক্ষেত্রটির কর্ণের দৈর্ঘ্য হবে √(3² + 2²) একক বা √13 একক।
আয়তক্ষেত্রের কর্ণদ্বয় কি সমান? Are the hypotenuses of a rectangle equal?
আয়তক্ষেত্রের প্রতিটি কোণ ৯০°। বিপরীত বাহুগুলো দৈর্ঘ্যে পরস্পর সমান। বিপরীত বাহুগুলো সমান্তরাল। কর্ণদ্বয় দৈর্ঘ্যে সমান এবং তারা পরস্পরকে সমদ্বিখন্ডিত করে।
আয়তক্ষেত্র সূত্র,
2(l + b)/2 বা l + b
l = দৈর্ঘ্য,
b = প্রস্থ।
আয়তক্ষেত্রের পরিধি নির্ণয়, Finding the Perimeter of a Rectangle :
একটি আয়তক্ষেত্রের পরিধি হল আয়তক্ষেত্রটির সীমা বা বাহু দ্বারা আচ্ছাদিত সম্পূর্ণ দূরত্ব। যেহেতু একটি আয়তক্ষেত্রের চারটি বাহু থাকে, তাই আয়তক্ষেত্রের পরিধি হবে চারটি বাহুর প্রতিটির পরিমাণ। আয়তক্ষেত্রের পরিধির একক হবে মিটার, সেন্টিমিটার, ইঞ্চি, ফুট ইত্যাদিতে।
পরিধি মূলত আয়তক্ষেত্রের সীমানা ছাড়া আর কিছুই নয়। 4টি বাহু যোগ করলে আমরা আয়তক্ষেত্রের পরিসীমা পাব। মনে করা যাক,
প্রতি বাহুর সমষ্টি = L+ L+ B + B
তবে, আয়তক্ষেত্রের পরিধি হবে = 2(L + B)
তির্যক দ্বারা একটি আয়তক্ষেত্রের ক্ষেত্রফল নির্ণয়, Find the area of a rectangle by the diagonal :
একটি আয়তক্ষেত্রের তির্যক হল আয়তক্ষেত্রের ভিতরে থাকা সরল রেখা যা তার বিপরীত শীর্ষগুলিকে যোগ করে। আয়তক্ষেত্রে দুটি কর্ণ থাকে এবং উভয়ই সমান দৈর্ঘ্যের। আমরা পিথাগোরাস উপপাদ্য ব্যবহার করে একটি আয়তক্ষেত্রের তির্যক বের করতে পারি।
(কর্ণ) 2 = (দৈর্ঘ্য) 2 + (প্রস্থ) 2
(দৈর্ঘ্য) 2 = (কর্ণ) 2 – (প্রস্থ) 2
দৈর্ঘ্য = √{(কর্ণ) 2 – (প্রস্থ) 2 }
এখন, একটি আয়তক্ষেত্রের ক্ষেত্রফল নির্ণয়ের সূত্রটি হল দৈর্ঘ্য × প্রস্থ। বিকল্পভাবে, আমরা এই সূত্রটিকে √{(কর্ণ) 2 – (প্রস্থ) 2 } × প্রস্থ হিসাবে লিখতে পারি ।
একটি আয়তক্ষেত্রের ক্ষেত্রফল = প্রস্থ (√{(কর্ণ) 2 – (প্রস্থ) 2 })।
শেষ কথা, Conclusion :
শিক্ষাক্ষেত্রে বিভিন্ন সূত্র মনে রাখতে হয়। বিশেষ করে গণিতের ক্ষেত্রে বেশিরভাগ প্রশ্নের সমাধান করতে গিয়ে সূত্র জেনে রাখা জরুরী। নয়তো বিভিন্নভাবে চেষ্টা করেও সমাধান পাওয়া যায় না, তাছাড়া কিছু প্রশ্নের ক্ষেত্রে সূত্র ব্যবহার না করলে তো অংক কষা শুরু হয় না।
গণিতের বিভিন্ন সূত্রের মধ্যে আয়তক্ষেত্রের পরিসীমা সূত্র জেনে রাখাও জরুরী। তাই আজকের এই প্রতিবেদনে আমরা আয়তক্ষেত্র সংক্রান্ত বেশ কিছু সূত্র তুলে ধরেছি।
এতে শিক্ষার্থীদের ক্ষেত্রে যেমন সুবিধা হবে তেমনি অন্যদের ক্ষেত্রেও বিভিন্ন কাজে সহায়তা হতে পারে। এই ধরনের তথ্যমূলক প্রতিবেদন আরো পেতে চাইলে চোখ রাখুন আমাদের ওয়েবসাইটে।
Frequently Asked Questions
উত্তর: যে চতুর্ভুজের বিপরীত বাহুগুলো পরস্পর সমান এবং প্রত্যেকটি কোণ সমকোণ তাকে আয়তক্ষেত্র বলে।
উত্তর: আয়তক্ষেত্রের পরিসীমা = ২(দৈর্ঘ্য + প্রস্থ)
উত্তর: আয়তক্ষেত্রের কর্ণের দৈর্ঘ্য নির্ণয়ের সূত্রটি হল √{(দৈর্ঘ্য)² + (প্রস্থ)²}
উত্তর: আয়তক্ষেত্রের ক্ষেত্রফল = (দৈর্ঘ্য × প্রস্থ) বর্গ একক।