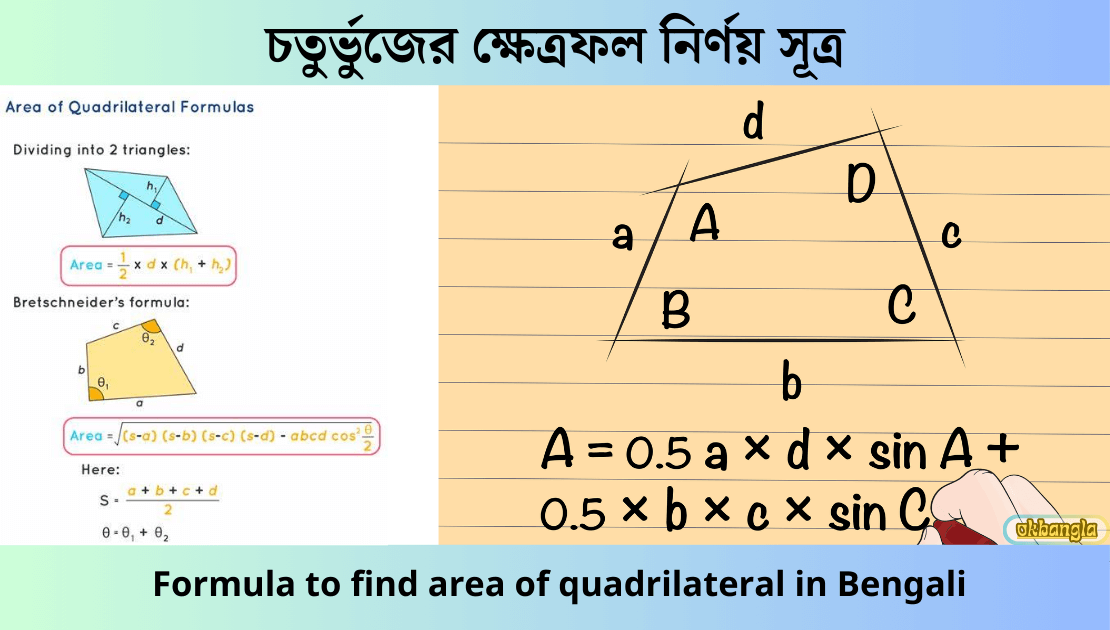
চতুর্ভুজের ক্ষেত্রফল হল একটি চতুর্ভুজের ভিতরে থাকা অংশের পরিমাণ। তবে প্রথমে জানতে হবে যে, চতুর্ভুজ কী? এক কথায় বলতে গেলে চতুর্ভুজ হল চারটি রেখার অংশ দ্বারা আবদ্ধ একটি বদ্ধ আকৃতি। চতুর্ভুজের ক্ষেত্রফল বের করার বিভিন্ন ধরনের সূত্র রয়েছে। আজকের এই প্রতিবেদনে আমরা চতুর্ভুজের ক্ষেত্রফলের সূত্র নিতে আলোচনা করব।
চতুর্ভুজের কয়টি দিক আছে? How many sides does a quadrilateral have?
“চতুর্ভুজ” শব্দটি ল্যাটিন শব্দ কোয়াড্রি থেকে এসেছে, যার অর্থ “চার”, এবং ল্যাটাস, যার অর্থ “পার্শ্ব”। একটি চতুর্ভুজকে চারটি বাহু , চারটি শীর্ষবিন্দু এবং চারটি কোণ সহ একটি দ্বি-মাত্রিক আকৃতি হিসাবে সংজ্ঞায়িত করা হয়।
চতুর্ভুজের ৭ প্রকার কি কি? What are the 7 types of quadrilaterals?
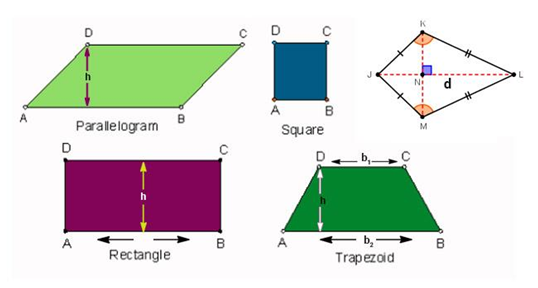
চতুর্ভুজ হল একটি দ্বি-মাত্রিক আকৃতি যার চারটি বাহু রয়েছে। সাতটি বিভিন্ন ধরণের চতুর্ভুজ রয়েছে: সমান্তরাল, রম্বস, কাইট, আয়তক্ষেত্র, ট্র্যাপিজয়েড, বর্গক্ষেত্র এবং সমদ্বিবাহু ট্র্যাপিজয়েড। প্রতিটি প্রকারের বিভিন্ন বৈশিষ্ট্য রয়েছে যা তাদের চারটি দিক থাকা ছাড়াও প্রয়োজন।
চতুর্ভুজের বৈশিষ্ট্য, Characteristics of Quadrilateral :
বিভিন্ন আকারের চতুর্ভুজগুলির বিভিন্ন গুণ রয়েছে এবং এই বৈশিষ্ট্যগুলির মধ্যে কিছু তাদের অনন্য করে তোলে। তবে সমস্ত চতুর্ভুজের অভ্যন্তরীণ কোণের সমষ্টি একই হবে। চতুর্ভুজের প্রত্যেকটিরই স্বতন্ত্র বৈশিষ্ট্য রয়েছে। তবে সকল প্রকার চতুর্ভুজের কিছু সাধারণ বৈশিষ্ট্য রয়েছে, সেগুলি হল :
- একটি বদ্ধ চিত্রের চারটি দিক রয়েছে।
- একটি চতুর্ভুজের অভ্যন্তরীণ কোণের সমষ্টি হল 360 ডিগ্রি।
- চতুর্ভুজের প্রকারের উপর নির্ভর করে চারটি বাহু দৈর্ঘ্যে পরিবর্তিত হতে পারে বা সমান হতে পারে।
যে চতুর্ভুজের চারটি বাহু অসমান তাকে কি বলে? What is the name of a quadrilateral whose four sides are unequal?
সামন্তরিক হল একটি চতুর্ভুজ। সামান্তরিকের প্রতিটি কোণ সমকোণ হলে তাকে আয়তক্ষেত্র বলে। আর যখন সামান্তরিকের চারটি বাহুই সমান, তখন এর নাম রম্বস। বর্গক্ষেত্র হল একই সাথে রম্বস ও আয়তক্ষেত্র।
চতুর্ভুজের ক্ষেত্রফল কী? What does the area of a quadrilateral mean?
চতুর্ভুজের ক্ষেত্রফল হল চতুর্ভুজের পার্শ্ব দ্বারা ঘেরা অঞ্চল। এটি বর্গ এককে পরিমাপ করা হয়। ক্ষেত্রফলের একক চতুর্ভুজের ক্ষেত্রফল বের করার প্রক্রিয়া নির্ভর করে তার প্রকার এবং চতুর্ভুজ সম্পর্কে উপলব্ধ তথ্যের উপর।
চতুর্ভুজের পরিধি কত? What is the perimeter of the quadrilateral?
চতুর্ভুজের পরিধি হল চতুর্ভুজের সব বাহুর দৈর্ঘ্যের সমষ্টি । চতুর্ভুজের পরিধি = চতুর্ভুজের সব বাহুর সমষ্টি। ধরুন ABCD একটি চতুর্ভুজ, ABCD = (AB+ BC + CD + DA) এককের পরিধি।
চতুর্ভুজ আকৃতির পরিধি নির্ণয় :
একটি চতুর্ভুজের পরিধি খুঁজে পেতে, আমাদের চারটি বাহুর সমস্ত দৈর্ঘ্য যোগ করতে হবে, অর্থাৎ, ABCD চতুর্ভুজের পরিধি = সমস্ত বাহুর দৈর্ঘ্যের সমষ্টি = AB +BC + CD + DA।
চতুর্ভুজের কর্ণ নির্ণয়ের সূত্র, Formula for determining the diagonal of a quadrilateral
আয়তক্ষেত্রের প্রস্থ একটি আয়তক্ষেত্র সূত্রের কর্ণে “w” অক্ষর দ্বারা নির্দেশিত হয়। সমীকরণটি d = (l² + w²) হিসাবে প্রকাশ করা হয়, যেখানে l এবং w যথাক্রমে আয়তক্ষেত্রের দৈর্ঘ্য এবং প্রস্থ।
চতুর্ভুজের ক্ষেত্রফল নির্ণয় সূত্র, Formula to find area of quadrilateral :
নিম্নে চতুর্ভুজের ক্ষেত্রফল নির্ণয় করার বিভিন্ন সূত্র উল্লেখ করা হল :
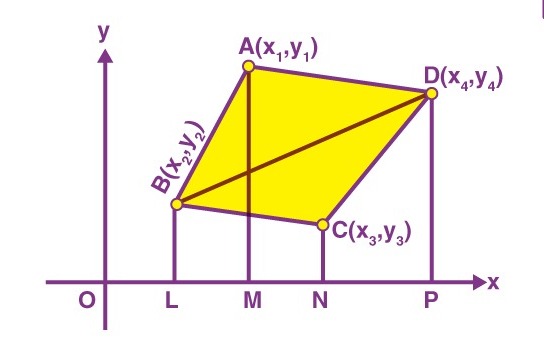
>> ত্রিভুজের ক্ষেত্রফল ব্যবহার করে চতুর্ভুজের ক্ষেত্রফল নির্ণয় করার সূত্র হল :
চতুর্ভুজের ক্ষেত্রফল ABCD = ত্রিভুজের ক্ষেত্রফল ABD + ত্রিভুজ BCD-এর ক্ষেত্রফল।
>> চতুর্ভুজের ক্ষেত্রফল নির্ণয় সূত্র
(1/2) × [(x 1 y 2 + x 2 y 3 + x 3 y 4 + x 4 y 1 ) – (x 2 y 1 + x 3 y 2 + x 4 y 3 + x1 বছর 4 )]
যেখানে (x 1 , y 1 ), (x 2 , y 2 ), (x 3 , y 3) ), এবং ( x 4 , y 4 ) একটি চতুর্ভুজের শীর্ষবিন্দু।
>> যদি এর একটি কর্ণ এবং শীর্ষবিন্দু থেকে উভয় লম্ব দেওয়া হয়, সেক্ষেত্রে চতুর্ভুজের ক্ষেত্রফল নির্ণয় করা যায় যেভাবে,
শীর্ষবিন্দু থেকে কর্ণ(d) এবং উভয় লম্বের দৈর্ঘ্য (h, H) দেওয়া হয়, তখন চতুর্ভুজের ক্ষেত্রফল সূত্র দ্বারা গণনা করা হয়: চতুর্ভুজের ক্ষেত্রফল = (½) × d × (h + H)
>> ট্রাপিজিয়ামের ক্ষেত্রফল = ১/২ X (সমান্তরাল বাহুদ্বয়ের যোগফল X সমান্তরাল বাহুদ্বয়ের মধ্যবর্তী লম্ব দূরত্ব)
>> বর্গক্ষেত্র : একটি বর্গক্ষেত্রের ক্ষেত্রফল হল এর দ্বারা দখলকৃত স্থান বা পৃষ্ঠের পরিমাপ। এটি একটি চারমুখী চতুর্ভুজ যার সবগুলো বাহু সমান, যার ক্ষেত্রফল সূত্র তার দুই বাহুর দৈর্ঘ্যের গুণফলের সমান, বর্গাকার চতুর্ভুজের ক্ষেত্রফল = (পার্শ্ব)²
>> রম্বস : একটি রম্বস হল একটি চারমুখী চতুর্ভুজ যার ক্ষেত্রফল কর্ণগুলির দৈর্ঘ্যের অর্ধেক গুণফলের সমান। একটি রম্বস আকৃতির চতুর্ভুজের ক্ষেত্রফল = (1 ⁄ 2) × কর্ণের গুণফল।
>> সমান্তরাল বৃত্ত : একটি সমান্তরালগ্রামের ক্ষেত্রফলকে দ্বি-মাত্রিক সমতলে সমান্তরাল বৃত্ত দ্বারা আচ্ছাদিত স্থানের পরিমাণ হিসাবে সংজ্ঞায়িত করা হয়। সমান্তরাল চতুর্ভুজ একটি বিশেষ ধরনের চতুর্ভুজ। এটি একটি চার-পার্শ্বযুক্ত চতুর্ভুজ যার ক্ষেত্রফল সূত্রটি এর ভিত্তি এবং উচ্চতার গুণফল হিসাবে প্রকাশ করা হয়, সমান্তরাল চতুর্ভুজের ক্ষেত্রফল নির্ণয় করার সূত্র হল = ভিত্তি × উচ্চতা
>> আয়তক্ষেত্র : আয়তক্ষেত্রের ক্ষেত্রফল হল আয়তক্ষেত্রের সীমানার মধ্যে আচ্ছাদিত একক বর্গের সংখ্যা। এটি আয়তক্ষেত্র হল একটি চার-পার্শ্বযুক্ত চতুর্ভুজ যার বিপরীত বাহু সমান। এর ক্ষেত্রফলকে এর দৈর্ঘ্য এবং প্রস্থের গুণফল হিসাবে প্রকাশ করা হয়, একটি আয়তক্ষেত্র আকৃতির চতুর্ভুজের ক্ষেত্রফল নির্ণয় করার সূত্র হল = দৈর্ঘ্য × প্রস্থ।
চতুর্ভুজটি যদি বর্গ, আয়তক্ষেত্র, রম্বস, সামান্তরিক বা ট্রাপিজিয়াম হয় তাহলে এগুলোর ক্ষেত্রফল উপরে উল্লেখিত সূত্রের মাধ্যমে নির্ণয় করা যায়। কিন্তু চতুর্ভুজটি যদি অনিয়মিত হয়, তবে তার ক্ষেত্রফল নির্ণয়ের জন্য সমাকলন পদ্ধতি প্রয়োগ করতে হয়।
বর্গক্ষেত্রের তির্যক নির্ণয়? Finding the diagonal of a square
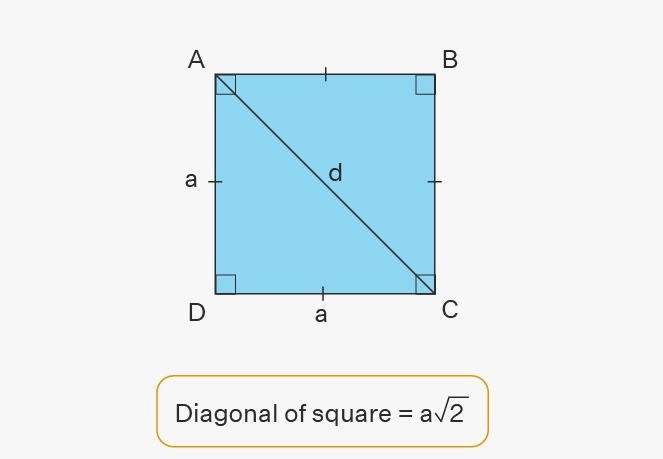
একটি বর্গক্ষেত্রের কর্ণের সূত্র হল d = a√2 , যেখানে’d’ হল কর্ণ এবং ‘a’ হল বর্গক্ষেত্রের বাহু। পিথাগোরাস উপপাদ্যটি বর্গক্ষেত্রের তির্যকের সূত্র খুঁজে বের করতে ব্যবহৃত হয়। একটি তির্যক একটি বর্গক্ষেত্রকে দুটি সমকোণী ত্রিভুজে ভাগ করে যা সমদ্বিবাহু।
শেষ কথা, Conclusion :
বিভিন্ন পরামিতির বৈশিষ্ট্যের উপর নির্ভর করে চতুর্ভুজের বিভিন্ন প্রকার রয়েছে। বিভিন্ন চতুর্ভুজ এলাকা সূত্র তাদের প্রকারের উপর নির্ভর করে। আশা করি আজকের এই প্রতিবেদনে উল্লেখ করা তথ্যগুলো থেকে আপনারা চতুর্ভুজের ক্ষেত্রফল নির্ণয় করার সূত্র সম্পর্কে ধারণা পেয়েছেন। এগুলো বিভিন্নভাবে আমাদের কাজে লাগে, তাই উক্ত সূত্রগুলো জেনে রাখা প্রয়োজন। বিভিন্ন ক্ষেত্রে দেখা যায় যে, চতুর্ভুজ এবং তাদের এলাকার নকশা, কৃষি এবং স্থাপত্যের ক্ষেত্রে অনেক ব্যবহারিক প্রয়োগ রয়েছে।
Frequently Asked Questions
চতুর্ভুজের ক্ষেত্রফল হল চতুর্ভুজের সীমানার ভিতরের অঞ্চল। এটি বর্গ এককে পরিমাপ করা হয়।
নিচে দেওয়া সূত্র ব্যবহার করে চতুর্ভুজের ক্ষেত্রফল পাওয়া যায়:
চতুর্ভুজের ক্ষেত্রফল = (1/2) × [(x 1 y 2 + x 2 y 3 + x 3 y 4 + x 4 y 1 ) – (x 2 y 1 + x 3 y 2 + x 4 y 3 + x1 বছর 4 )]
যেখানে (x 1 , y 1 ), (x 2 , y 2 ), (x 3 , y 3) ), এবং ( x 4 , y 4 ) একটি চতুর্ভুজের শীর্ষবিন্দু।
বিভিন্ন ধরনের চতুর্ভুজ হল: বর্গক্ষেত্র, আয়তক্ষেত্র, রম্বস, ঘুড়ি, সমান্তরাল বৃত্ত, ট্রাপিজিয়াম।