🏆 আজকের ফ্রি বাংলা কুইজ খেলুন এবং Gift Voucher পুরস্কারের জেতার সুযোগ নিন।
Play Now
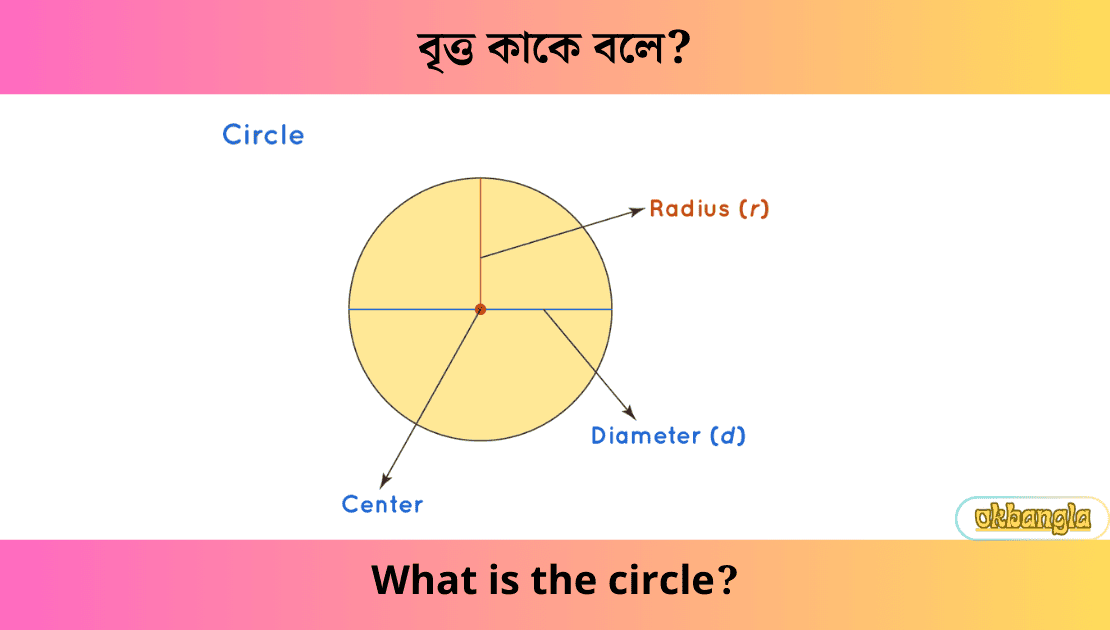
বৃত্ত হল একটি সমতলীয় জ্যামিতিক চিত্র যার সকল বিন্দু একটি নির্দিষ্ট বিন্দু থেকে সমান দূরত্বে অবস্থিত। এই নির্দিষ্ট বিন্দুটিকে বলা হয় বৃত্তের কেন্দ্র। কেন্দ্র থেকে বৃত্তের যেকোনো বিন্দু পর্যন্ত দূরত্বকে বলা হয় বৃত্তের ব্যাসার্ধ।
বৃত্ত আবিষ্কারের ইতিহাস, History of the discovery of circle:
বৃত্ত, গণিতের সবচেয়ে মৌলিক আকারগুলির মধ্যে একটি। এর নিখুঁত গোলাকার আকৃতি এবং সৌন্দর্য মানুষকে সর্বদা মুগ্ধ করেছে। কিন্তু বৃত্তের ব্যবহার কবে থেকে শুরু হয়েছিল, এমন প্রশ্ন অনেকের মনেই জাগে।
বৃত্ত আবিষ্কারের কোনো নির্দিষ্ট ব্যক্তির নাম নেই। বরং এটি মানুষের প্রাকৃতিক পরিবেশ পর্যবেক্ষণের ফল। চাঁদ, সূর্য, গাছের পাতা, পাথরের গোল গোল আকার – এই সবকিছু মানুষকে বৃত্তের ধারণা দিয়েছে।
- প্রাচীন সভ্যতায় বৃত্ত: মিশরীয়রা, ব্যাবিলনীয়রা, গ্রীকরা সকলেই বৃত্তের গুরুত্ব বুঝত। তারা পিরামিড, মন্দির, চাকা নির্মাণে বৃত্তের ব্যবহার করত।
- গণিত ও বিজ্ঞানে বৃত্ত: ইউক্লিডের ‘এলিমেন্টস’ গ্রন্থে বৃত্তের বিস্তারিত বর্ণনা পাওয়া যায়। আধুনিক গণিত, জ্যামিতি, ত্রিকোণমিতি – সব ক্ষেত্রেই বৃত্তের গুরুত্ব অপরিহার্য।
- দৈনন্দিন জীবনে বৃত্ত: চাকা, ঘড়ি, মুদ্রা, গোলাকার খাবারের পাত্র – আমাদের দৈনন্দিন জীবনে বৃত্তের ব্যবহার অসংখ্য।
মূল কথা হল বৃত্ত আবিষ্কার করা হয়নি, বরং মানুষ প্রকৃতি থেকে এই আকারটি আবিষ্কার করেছে এবং তারপর তা ব্যবহার করতে শিখেছে।
বৃত্তের গুরুত্ব, The importance of circle:
- প্রাকৃতিক সৌন্দর্য: বৃত্তের নিখুঁত আকার প্রকৃতির সৌন্দর্যের প্রতিফলন।
- গণিত ও বিজ্ঞানের ভিত্তি: বৃত্ত গণিতের অনেক ধারণার ভিত্তি।
- দৈনন্দিন জীবনের সুবিধা: চাকার আবিষ্কার মানুষের জীবনকে বদলে দিয়েছে।
- কলা ও সাহিত্যে: বৃত্ত বিভিন্ন কলা ও সাহিত্যকর্মে প্রতীক হিসেবে ব্যবহৃত হয়।
বৃত্ত একটি আদিম আকার যা মানুষের সঙ্গে অবিচ্ছেদ্যভাবে জড়িত। এর ব্যবহার কবে থেকে শুরু হয়েছে, তা নির্দিষ্ট করে বলা যায় না। তবে মানুষের প্রাচীন সভ্যতা থেকে আজকের আধুনিক যুগ পর্যন্ত বৃত্তের গুরুত্ব কখনো কমেনি।
বৃত্তের বিভিন্ন অংশ, Different parts of circle :
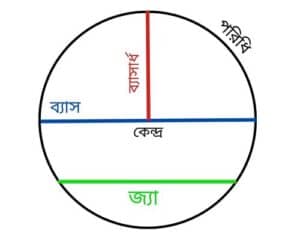
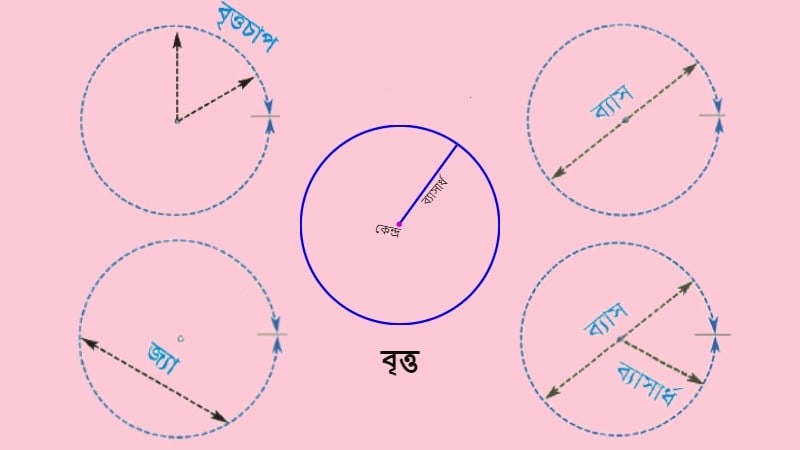
- ব্যাস: বৃত্তের কেন্দ্র দিয়ে যাওয়া এবং বৃত্তকে দুটি সমান অংশে ভাগ করা একটি রেখাখণ্ডকে ব্যাস বলে। ব্যাসের দৈর্ঘ্য ব্যাসার্ধের দ্বিগুণ।
- জ্যা: বৃত্তের যেকোনো দুটি বিন্দুকে যোগ করা রেখাখণ্ডকে জ্যা বলে। ব্যাস হল সবচেয়ে বড় জ্যা।
- স্পর্শক: বৃত্তকে একটি বিন্দুতে ছেদ করে এমন একটি রেখাকে স্পর্শক বলে। স্পর্শক বিন্দুতে বৃত্তের ব্যাসার্ধ স্পর্শকের উপর লম্ব হয়।
- বৃত্তচাপ: বৃত্তের পরিধির একটি অংশকে বৃত্তচাপ বলে।
- বৃত্তের গুরুত্বপূর্ণ সূত্র
- পরিধি: বৃত্তের পরিধি (C) = 2πr (যেখানে, r হল ব্যাসার্ধ এবং π হল একটি ধ্রুবক যার মান প্রায় 22/7 বা 3.1416)
- ক্ষেত্রফল: বৃত্তের ক্ষেত্রফল (A) = πr²
বৃত্তের পরিভাষা, Circle terminology :
একটি বৃত্তের সাথে সম্পর্কিত বিভিন্ন জ্যামিতিক উপাদানের নাম ও ব্যাখ্যা নিম্নরূপ:
- অ্যানুলাস (Annulus): দুটি সমকেন্দ্রিক বৃত্ত দ্বারা সীমাবদ্ধ একটি বলয়াকার অঞ্চল।
- চাপ (Arc): বৃত্তের যেকোনো সংযুক্ত অংশ। একটি চাপের দুটি প্রান্তিক বিন্দু এবং কেন্দ্র নির্দিষ্ট করলে, দুটি চাপ পাওয়া যায় যা একত্রে একটি পূর্ণ বৃত্ত গঠন করে।
- কেন্দ্র (Centre): বৃত্তের উপরের সমস্ত বিন্দু থেকে সমদূরবর্তী বিন্দু।
- জ্যা (Chord): একটি রেখাংশ যার প্রান্তিক বিন্দু দুটি বৃত্তের উপর অবস্থিত এবং বৃত্তটিকে দুটি খণ্ডে বিভক্ত করে।
- পরিধি (Circumference): বৃত্তের চারপাশের দৈর্ঘ্য বা বৃত্ত বরাবর একবার ঘুরে আসার দূরত্ব।
- ব্যাস (Diameter): একটি রেখাংশ যার প্রান্তিক বিন্দু দুটি বৃত্তের উপর অবস্থিত এবং কেন্দ্রটির মধ্য দিয়ে যায়; অথবা এমন একটি রেখাংশের দৈর্ঘ্য। এটি বৃত্তের উপরের যেকোনো দুটি বিন্দুর মধ্যে সর্বোচ্চ দূরত্ব। এটি জ্যা-এর একটি বিশেষ ক্ষেত্র, যথা, একটি নির্দিষ্ট বৃত্তের সর্ববৃহৎ জ্যা এবং এর দৈর্ঘ্য ব্যাসার্ধের দৈর্ঘ্যের দ্বিগুণ।
- চক্রিকা (Disc): একটি বৃত্ত দ্বারা সীমাবদ্ধ সমতলের অঞ্চল। কঠোর গাণিতিক ব্যবহারে, বৃত্ত শুধুমাত্র চক্রিকার সীমা নির্দেশ করে, তবে দৈনন্দিন ব্যবহারে “বৃত্ত” শব্দটি চক্রিকাও বোঝাতে পারে।
- লেন্স (Lens): দুটি উপরিপাতী চক্রিকার সাধারণ অঞ্চল (ছেদ)।
- ব্যাসার্ধ (Radius): বৃত্তের কেন্দ্রকে বৃত্তের উপরের যেকোনো একটি বিন্দুর সাথে যোগ করা একটি রেখাংশ; অথবা এমন একটি রেখাংশের দৈর্ঘ্য, যা ব্যাসের (দৈর্ঘ্যের) অর্ধেক। সাধারণত, ব্যাসার্ধকে r দ্বারা চিহ্নিত করা হয় এবং একটি ধনাত্মক সংখ্যা হতে হবে। r = 0 সম্পন্ন একটি বৃত্ত একটি নির্বিকার ক্ষেত্র যা একটি একক বিন্দু দ্বারা গঠিত।
- কোণক (Sector): সমান দৈর্ঘ্যের দুটি ব্যাসার্ধ দ্বারা সীমাবদ্ধ একটি অঞ্চল যার সাধারণ কেন্দ্র রয়েছে এবং এই কেন্দ্র এবং ব্যাসার্ধের প্রান্তিক বিন্দু দ্বারা নির্ধারিত দুটি সম্ভাব্য চাপের যেকোনো একটি।
- খণ্ড (Segment): একটি জ্যা এবং জ্যা-এর প্রান্তিক বিন্দু দুটিকে সংযুক্তকারী চাপগুলির মধ্যে যেকোনো একটি দ্বারা সীমাবদ্ধ একটি অঞ্চল। জ্যা-এর দৈর্ঘ্য সম্ভাব্য চাপগুলির ব্যাসের জন্য একটি নিম্ন সীমা আরোপ করে। কখনও কখনও খণ্ড শব্দটি শুধুমাত্র সেই অঞ্চলগুলির জন্য ব্যবহৃত হয় যা তাদের চাপের অন্তর্গত বৃত্তের কেন্দ্র ধারণ করে না।
- ছেদক (Secant): একটি প্রসারিত জ্যা, একটি সমতলীয় সরলরেখা, যা একটি বৃত্তকে দুটি বিন্দুতে ছেদ করে।
- অর্ধবৃত্ত (Semicircle): ব্যাসের প্রান্তিক বিন্দু দুটি দ্বারা নির্ধারিত দুটি সম্ভাব্য চাপের মধ্যে যেকোনো একটি, যা এর মধ্যবিন্দুকে কেন্দ্র হিসাবে গ্রহণ করে। অতার্তিক সাধারণ ব্যবহারে এর অর্থ হতে পারে একটি ব্যাস এবং এর একটি চাপ দ্বারা সীমাবদ্ধ দ্বি-মাত্রিক অঞ্চলের অভ্যন্তর, যাকে কারিগরিভাবে অর্ধচক্রিকা বলা হয়। অর্ধচক্রিকা একটি বিশেষ ধরনের খণ্ড, যথা, সর্ববৃহৎ খণ্ড।
- স্পর্শক (Tangent): একটি সমতলীয় সরলরেখা যার একটি বৃত্তের সাথে একটিমাত্র সাধারণ বিন্দু রয়েছে (“এই বিন্দুতে বৃত্তকে স্পর্শ করে”)।
বৃত্তের ব্যবহার, Use of circles :
বৃত্ত আমাদের দৈনন্দিন জীবনে বিভিন্নভাবে ব্যবহৃত হয়। যেমন:
- চাকা
- গোলক
- ঘড়ির মুখ
- পিজ্জা
- সূর্য
- চাঁদ
বৃত্ত সম্পর্কিত আরো কিছু তথ্য :
- একটি বৃত্তের সকল জ্যা বৃত্তের কেন্দ্র দিয়ে যায় না।
- একটি বৃত্তের অসংখ্য স্পর্শক আঁকা যায়।
- একটি বৃত্তের কেন্দ্র থেকে যেকোনো জ্যার উপর অঙ্কিত লম্ব জ্যাকে দুটি সমান ভাগে ভাগ করে।
গাণিতিকভাবে বৃত্ত পরিমাপের উপায় :
বৃত্তকে গাণিতিকভাবে পরিমাপ করার জন্য আমরা কয়েকটি নির্দিষ্ট পরিমাপ ব্যবহার করি। এই পরিমাপগুলো হল:
- ব্যাসার্ধ (Radius): বৃত্তের কেন্দ্র থেকে যেকোনো বিন্দু পর্যন্ত সরলরেখার দূরত্বকে ব্যাসার্ধ বলে। একে সাধারণত r দ্বারা প্রকাশ করা হয়।
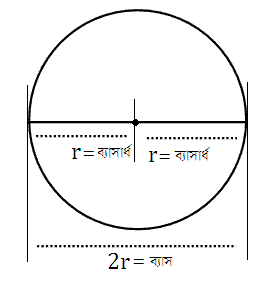
- ব্যাস (Diameter): বৃত্তের কেন্দ্র দিয়ে যাওয়া এবং বৃত্তকে দুটি সমান ভাগে ভাগ করে এমন একটি সরলরেখার দৈর্ঘ্যকে ব্যাস বলে। একে সাধারণত d দ্বারা প্রকাশ করা হয়। ব্যাস = 2 × ব্যাসার্ধ (d = 2r)
- পরিধি (Circumference): বৃত্তের চারপাশের দৈর্ঘ্যকে পরিধি বলে। একে সাধারণত C দ্বারা প্রকাশ করা হয়। পরিধি = 2π × ব্যাসার্ধ (C = 2πr), যেখানে π (পাই) একটি ধ্রুবক সংখ্যা যার মান প্রায় 3.1416।
- ক্ষেত্রফল (Area): বৃত্তের ভেতরের অংশের ক্ষেত্রফলকে বৃত্তের ক্ষেত্রফল বলে। একে সাধারণত A দ্বারা প্রকাশ করা হয়। ক্ষেত্রফল = π × (ব্যাসার্ধ)² (A = πr²)
বৃত্ত পরিমাপের জন্য ব্যবহৃত সূত্রগুলি:
- ব্যাস নির্ণয়: d = 2r
- পরিধি নির্ণয়: C = 2πr
- ক্ষেত্রফল নির্ণয়: A = πr²
উদাহরণ:
- যদি একটি বৃত্তের ব্যাসার্ধ 5 সেমি হয়, তাহলে তার ব্যাস হবে 2 × 5 সেমি = 10 সেমি।
- ওই বৃত্তের পরিধি হবে 2 × 3.1416 × 5 সেমি ≈ 31.42 সেমি।
- আর ওই বৃত্তের ক্ষেত্রফল হবে 3.1416 × (5 সেমি)² ≈ 78.54 বর্গসেমি।
কোন পরিমাপ জানা থাকলে অন্য পরিমাপগুলি এই সূত্রগুলো ব্যবহার করে নির্ণয় করা যায়।
উপসংহার, Conclusion:
বৃত্ত গণিতের একটি মৌলিক আকৃতি এবং এর বিভিন্ন ব্যবহার রয়েছে। বৃত্ত সম্পর্কে জানা আমাদের অনেক গাণিতিক সমস্যা সমাধান করতে সাহায্য করে।